1) quaternion-Euler angle transforming


四元数欧拉角转换
2) Euler dynamics and quaternion


欧拉动力学和四元数法
3) Euler conversion formula


欧拉转换公式
1.
the article discusses the concept of progression convergence speed, introducing Euler conversion formula and its progression convergence accleration and the conditions that Euler conversion foumula accelerates the convergence of progression.
论述了级数收敛速度的概念 ,并介绍了欧拉转换公式及其级数加速收敛的技术 ,以及欧拉转换公式提高级数收敛速度的条件。
4) unit quaternion transformation


四元数变换
1.
According to its specific geometry, a parameterized equation of forward position analysis was constructed under single orthogonal geometry by using unit quaternion transformation.
根据纯转动型 3 UPU并联机构的几何特点 ,使用四元数变换方法 ,构造了一类单正交条件下的 3 UPU并联机构位置正解分析的参数化方程 ,可使用三角恒等变换来求解该方程 ;并使用单位四元数变换求出其双正交条件下的 8个封闭的位置正解 ,该正解为 4组共轭
5) commutative quaternion algebra


可换四元数
1.
In this paper,we study the Riemann-Hilbert boundary value problem on the unit disk for a class of first order hyperbolic equation in commutative quaternion algebra.
为考察高维双曲方程的边值问题,本文引进可换四元数空间,并在此空间中讨论了可换四元数代数中一类一阶双曲方程的Riemann-Hilbert边值问题,我们获得了在指标非负的情况下唯一解的一般形式,以及在有指标小于零时代不同情况下Riemann-Hilbert边值问题的可解条件。
2.
In this paper,the Riemann-Hilbert boundary value problem for a class of first order hyperbolic equation in commutative quaternion algebra is considered,and the general solutions and the solvable conditions of the problem in different cases are obtained.
讨论了可换四元数代数中一类一阶双曲方程的Riemann-Hilbert边值问题。
6) Euler-axis rotation parameters


欧拉轴旋转参数
1.
A detailed survey is presented of the methods of rigid-body attitude representation, including Euler angles, the Euler-axis rotation parameters, the direction cosines and the Euler-Rodrigues quaternion.
首先论述了姿态描述的四种方法:欧拉角、欧拉轴旋转参数、方向余弦和四元数法,重点介绍了四元数法在飞行器运动学上的应用,它消除了欧拉方程的奇异性,计算效率也远远优于其他三种方法;最后讨论了数值仿真的方法及误差。
补充资料:欧拉角
| 欧拉角 Eulerian angles 用来确定定点转动刚体位置的3个一组独立角参量,由章动角θ、旋进角(即进动角)ψ和自转角j组成。为欧拉首先提出而得名。它们有多种取法,下面是常见的一种。如图所示,由定点O作出固定坐标系Oxyz和固连于刚体的动坐标系Ox′y′z′。以轴Oz和Oz′为基本轴,其垂直面Oxy和Ox′y′为基本平面。由轴Oz量到Oz′的角θ称章动角。平面zOz′的垂线ON称节线,它又是基本平面Ox′y′和Oxy的交线。在右手坐标系中,由ON的正端看,角θ应按逆时针方向计量。由固定轴Ox量到节线ON的角ψ称旋进角;由节线ON量到动轴Ox′的角j称自转角。由轴Oz和Oz′正端看,角ψ和j也都按逆时针方向计量。若令Ox′y′z′的初始位置与Oxyz重合,经过相继绕Oz、ON和Oz′的三次转动后,刚体将转到图示的任意位置。如果刚体绕通过定点O的某一轴线以角速度ω转动,而ω在动坐标系Ox′y′z′上的投影为ωx′、ωy′、ωz′,则它们可用欧拉角及其微商表示如下:ωx′= 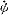 sinθsinj+ sinθsinj+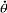 cosj,ωy′= cosj,ωy′=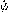 sinθcosj- sinθcosj- sinj,ωz′= sinj,ωz′=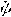 cosθ+ cosθ+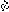 。如果已知ψ、θ、j和时间的关系,则可用上式计算ω在动坐标轴上的3个分量;反之,如已知任一瞬时t的ω各个分量,也可利用上式求出ψ、θ、j和时间t的关系,因而也就决定了刚体的运动。上式通常被称为欧拉运动学方程。 。如果已知ψ、θ、j和时间的关系,则可用上式计算ω在动坐标轴上的3个分量;反之,如已知任一瞬时t的ω各个分量,也可利用上式求出ψ、θ、j和时间t的关系,因而也就决定了刚体的运动。上式通常被称为欧拉运动学方程。
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
