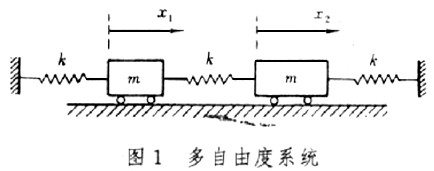
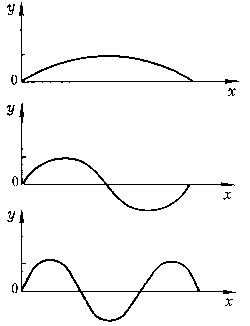
1) van der Pol non-linear vibration system
van der Pol非线性振动系统
2) Duffing-van der Pol non-linear vibration system
Duffing-van der Pol非线性振动系统
3) van der Pol oscillator
van der Pol振子
1.
Amplitude control of limit cycle of coupled van der Pol oscillator;
耦合的van der Pol振子的极限环幅值控制
4) Duffing-van der Pol system
Duffing-van der Pol系统
1.
Based on the active control method of chaotic system,the problem of chaotic synchronization of the extended Duffing-Van der Pol systems with different initial conditions and different parametric conditions is investigated.
基于混沌系统的主动控制同步方法,研究了具有不同初始条件以及不同参数条件的扩展Duffing-Van der Pol系统混沌轨道的同步问题。
2.
Symmetry-breaking bifurcation in a double-well Duffing-Van der pol system with bounded random parameter under harmonic excitations,is investigated.
讨论谐和激励作用下含有界随机参数的双势井Duffing-Van der pol系统的对称破裂分岔现象。
5) Van der P ol Duffing oscillator
Van-der-Pol Duffing系统
6) stochastic van der Pol system
随机van der Pol系统
1.
Investigation of the bifurcation of stochastic van der Pol system;
双边约束条件下随机van der Pol系统的分岔研究
2.
Period-doubling bifurcation analysis of stochastic van der Pol system via Chebyshev polynomial approximation;
基于Chebyshev多项式逼近的随机van der Pol系统的倍周期分岔分析
补充资料：线性振动
| 线性振动 linearvibration 系统中构件的弹性服从胡克定律，运动时产生的阻尼力与广义速度（广义坐标的时间导数）的一次式成正比的振动。它通常是实际系统微幅振动的一个抽象模型。线性振动系统适用叠加原理，即如果在输入x1作用下，系统响应为y1，而在输入x2作用下，系统响应为y2，则系统在输入x1和x2的联合作用下的响应就是y1＋y2。在叠加原理基础上，可把一个任意的输入分解为一系列微元冲量的和，然后求得系统的总响应；还可将一个周期激励经傅里叶变换，展成一系列谐和分量之和，分别考察各谐和分量对系统的作用结果，再将它们叠加起来，就得到系统的总响应。因此，常参量线性系统的响应特性可用脉冲响应或频率响应描述。脉冲响应指系统对单位冲量的响应，表征系统在时域内的响应特性。频率响应指系统对单位谐和输入的响应特性，表征系统在频域内的响应特性。两者由傅里叶变换确定对应关系。 单自由度系统的线性振动是可用一个广义坐标来确定系统位置的线性振动。它是最简单的振动，许多振动的基本概念和特征可由此引出。它包括简谐振动、自由振动、衰减振动和受迫振动。 多自由度系统的线性振动是自由度n≥2的线性系统的振动。图1
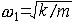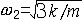 , ，每个频率对应一种振动形态。各简谐振子进行同频率的谐和振动，同步地通过平衡位置，又同步地到达极端位置，这种振动称为主振动。在对应于ω1的主振动中，有x1＝x2；在对应于ω2的主振动中，有x1＝－x2 。在主振动中各质量的位移之比保持一个确定的关系，构成一个确定的振型，称为主振型或固有振型。各主振型之间存在着关于质量与刚度的正交性，它反映各主振动之间的相互独立性。固有频率与主振型表征多自由度系统固有的振动特性。一个n自由度系统有n个固有频率和n个主振型。系统的任何振动形态都可以表示成各个主振型的线性组合。因此，在多自由度系统动态响应分析中，广泛采用主振型叠加法。于是，系统固有振动特性的测试和分析也就成为系统动态设计的一个常规步骤。多自由度系统的动态特性也可以用频率响应描述。由于各输入输出之间都有一个频率响应函数，从而构成一个频率响应矩阵。频率响应与主振型之间有确定的关系。和单自由度系统不同，多自由度系统的幅频特性曲线有多个共振峰。弹性体的线性振动是弹性体有无限多个自由度，因而具有无限多个固有频率和无限多个主振型。弹性体的任何振动形态也可表示为各主振型的线性叠加。因而对于弹性体的动态响应分析，主振型叠加法仍然适用。以弦的振动为例。设单位长度质量为m的细弦，长l，两端张紧 ，张力为T。弦的固有频率fn＝na／2l（n＝1，2，3，…），式中a＝（T／m）1/2，是横波沿弦线方向的传播速度。弦的各阶固有频率恰巧为基频a／2l的整数倍 。这种整数倍关系导致悦耳的谐音结构。一般弹性体各阶固有频率并不存在这种整数倍关系。张紧弦的前三阶振型如图2
所示。取一弦端为x轴原点 ，则对应第n阶固有频率fn的主振型为yn（x）＝Asin（nπx／l），式中A为振幅。主振型曲线上有一些节点，弦的第n阶主振型有n－1个节点。在主振动中，各节点不振动。弹性体的线性振动在数学上可归结为偏微分方程的边值问题。但只有在一些最简单的情况下才能找到准确解，因而对于复杂的弹性体的线性振动问题必须求助于近似解法。各种近似解法的要旨是变无限为有限，也就是将无限多自由度系统（连续系统）离散化为有限多个自由度系统（离散系统）。工程分析中广泛采用的离散化方法有两大类：有限元法与模态综合法。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条