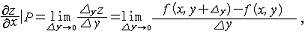1) Boolean partial derivative
布尔偏导数
1.
New method testing the double fault of combinational circuits based on Boolean partial derivative.;
基于布尔偏导数的组合电路双故障检测的新方法
2.
Tabular method of calculating Boolean partial derivative and difference of the OC type logic function.;
计算OC型逻辑函数的布尔偏导数与布尔差分的表格方法
3.
Methods of calculating Boolean partial derivative based on d_j-map.;
基于d_j图的逻辑函数布尔偏导数的计算方法
2) Boolean polarization-encoded logic algebra
布尔偏振编码逻辑代数
1.
In this paper,the Boolean polarization-encoded logic algebra(BPLA)is used to designoptical parallel array logic gates and liquid crystal encoded ripple-carry full adder.
本文报道了利用布尔偏振编码逻辑代数（ＢＰＬＡ）理论来设计光学并行阵列逻辑门及液晶编码脉动进位加法器的详细过程，最后给出了加法器的实验结果。
3) Partial derivative
偏导数
1.
A Principle of calculus partial derivative of homogenous polynomial of degree m;
关于m次齐次多项式偏导数的一个算法原理
2.
A Definition of Partial Derivative of Random Functions and Its Application to RBFNN Sensitivity Analysis;
随机意义下依概率测度收敛的偏导数的定义及在RBFNN的敏感性分析中的应用
3.
Modified method for matrix orthogonalization and its partial derivative
修正的矩阵正交化方法及其偏导数
4) e-partial derivative
e-偏导数
1.
In order to discuss the properties of Bent Function based on e-partial derivative and relationship of Bent Function and linear Function,the paper proposed a relatively simple algorithm no matter whether the Boolean Function is Bent Function or not.
为讨论Bent函数性质的需要,在研究了线性函数与Bent函数关系及e-偏导数的密码学性质的基础上,本文提出了一种判断布尔函数是否为Bent函数较容易的算法。
5) partial derivative method
偏导数法
1.
A computational scheme is presented to evaluate the dynamic stiffness and damping coefficients of the aerodynamic tilting-pad journal bearings by combining the partial derivative method with the equivalent coefficient method.
提出将偏导数法和折合系数法相结合来计算可倾瓦空气动压轴承的动态刚度和阻尼系数。
2.
A novel and universal computational method for obtaining the dynamic stiffness and dynamic damping coefficients of aerodynamic bearings is presented by means of the partial derivative method applied to the gas-lubricated Reynolds equation,and the dynamic stiffness and dynamic damping coefficients of a typical aerodynamic bearing are eva.
采用偏导数法求解动压气体润滑Reynolds方程,给出了动压气体轴承动态刚度和阻尼系数普遍适用的计算方法。
6) partial derivatives
偏导数
1.
We are familiar with the algorithm of the partial derivatives from the calculus.
对于数学分析教材中所讲到的求解多元函数的偏导数的方法,大家都很熟悉,但是在遇到比较复杂的函数形式时,求偏导数的复杂程度也会随着增加。
2.
This paper presents the method of designing active filters in which the first and second-order partial derivatives of the transfer function with respect to the time constant of the OA s vanish.
本文讨论了转移函数对运放时间常数τ_i=1/GB_i 的一阶与二阶偏导数为零的有源滤波器的设计方法。
3.
The filters are based on local partial derivatives.
该算法主要利用像素点的偏导数信息把所有的像素点分为有效的信号点和噪声点,判定的标准为:任意像素点的值如果在其邻域为最大或最小值,则认为该点是噪声点,否则就是有效点。
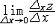存在且有限，就称此极限为二元函数
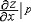，或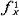
（x，y），类似地有