1) infinitesimal
[英][,ɪnfɪnɪ'tesɪml] [美]['ɪnfɪnə'tɛsəmḷ]


无穷小量
1.
The Extension and Application of the Equivalent Infinitesimal Replacement;


等价无穷小量代换的推广和应用
2.
An infinitesimal equivalence theorem is established in this paper.


建立了一个无穷小量等价的定理,文献1中的结果可作为本文定理的一个简单应用。
3.
This paper takes the infinitesimal as an entrance to derivative and shows the essential of derivative concept step by step and therefore enhances the students to comprehend this concept.
导数是高等数学中的一个重要概念,讨论了一种不同于目前多数教材中介绍导数概念的方法,以无穷小量为切入点,一步步过渡到导数的概念等,揭示了导数概念的本质,强化了学生对这一概念的理解。
2) infinitesimal quantity


无穷小量
1.
In this paper,the link between infinitesimal quantity and some important notions in differential and integral calculus,and the simple application of infinitesimal in limit operation are discussed.
讨论了无穷小量与微积分中几个重要概念的联系和无穷小在极限运算中的简单应用。
2.
In teaching mathematics, we should use geometric figures more in explaining concepts, attach importance to ratio limit and infinitesimal quantity, employ the regular methods, pay attention to the specific skills and help them analyze and solve problems.
在教学中应多用几何图形介绍概念;突出比值极限,重视无穷小量;立足常规方法;注意特殊技巧;引导学生分析、解决问题。
3) infinitely small quantity


无穷小量
1.
Theorem 1 and 2 about ratio of two infinitely small quantity function monotonous are obtained.
对文献[1]给出的一个函数单调性的判别命题进行推广,得出两个无穷小量之比的单调性的判别命题1,2。
2.
In this paper,we disscus the poerations of infinitely small quantity and get some result.


讨论了无穷个无穷小量作和、积运算后是否仍为无穷小量,得到的结论论是:无限个无穷小量的和、积未必收敛,即使收敛,也未必是无穷小量。
3.
In this note, we construct some examples to show that the infinitely product of the infinitely small quantity may be not infinitely small quantity.
本文由有限个无穷小量的乘积仍是无穷小量的证明入手 ,给出无穷多个无穷小量的乘积不一定是无穷小量的例子 ,并根据这种方法得到无穷多个无穷大量的和也不一定是无穷大量的结
4) infinite small quantity serie


无穷小量阶
5) infinitesimal increment


无穷小增量
6) higher order indefinite small


高阶无穷小量
补充资料:无穷小量
| 无穷小量 infinitesimal 以数零为极限的变量。确切地说,当自变量x无限接近x0(或x的绝对值无限增大)时,函数值f(x)与零无限接近,即 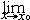 f(x)=0(或 f(x)=0(或 f(x)=0),则称f(x)为当x→x0(或x→∞)时的无穷小量。例如,f(x)=(x-1)2是当x→1时的无穷小量,f(n)= f(x)=0),则称f(x)为当x→x0(或x→∞)时的无穷小量。例如,f(x)=(x-1)2是当x→1时的无穷小量,f(n)=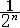 是当n→∞时的无穷小量,f(x)=sinx是当x→0时的无穷小量。特别要指出的是,切不可把很小的数与无穷小量混为一谈。 是当n→∞时的无穷小量,f(x)=sinx是当x→0时的无穷小量。特别要指出的是,切不可把很小的数与无穷小量混为一谈。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条