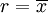标准差概述
标准差是一种表示分散程度的统计观念，主要是根据基金净值于一段时间内波动的情况计算而来的。标准差已广泛运用在股票以及共同基金投资风险的衡量上，主要是根据基金净值于一段时间内波动的情况计算而来的。一般而言，标准差愈大，表示净值的涨跌较剧烈，风险程度也较大。实务的运作上，您可进一步运用单位风险报酬率的概念，同时将报酬率的风险因素考虑在内。所谓单位风险报酬率是指衡量投资人每承担 一单位的风险，所能得到的报酬，以夏普指数最常为投资人运用。
标准差是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准差，代表大部分的数值和其平均值之间差异较大；一个较小的标准差，代表这些数值较接近平均值。
例如，两组数的集合 {0, 5, 9, 14} 和 {5, 6, 8, 9} 其平均值都是 7 ，但第二个集合具有较小的标准差。
标准差可以当作不确定性的一种测量。例如在物理科学中，做重复性测量时，测量数值集合的标准差代表这些测量的精确度。当要决定测量值是否符合预测值，测量值的标准差占有决定性重要角色：如果测量平均值与预测值相差太远（同时与标准差数值做比较），则认为测量值与预测值互相矛盾。这很容易理解，因为值都落在一定数值范围之外，可以合理推论预测值是否正确。
[编辑]标准差的简易计算公式
假设有一组数值 x1, ..., xN （皆为实数），其平均值为：
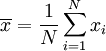
此组数值的标准差为：
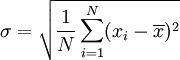
一个较快求解的方式为：
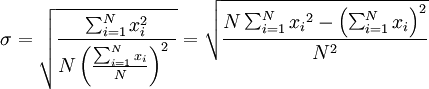
一随机变量X 的标准差定义为：
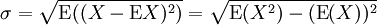
须注意并非所有随机变量都具有标准差，因为有些随机变量不存在期望值。 如果随机变量 X 为 x1,...,xN 具有相同机率，则可用上述公式计算标准差。从一大组数值当中取出一样本数值组合 x1,...,xn ，常定义其样本标准差：
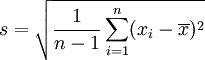
范例
这里示范如何计算一组数的标准差。例如一群孩童年龄的数值为 { 5, 6, 8, 9 } ：
第一步，计算平均值
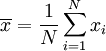
n = 4 （因为集合里有 4 个数），分别设为：
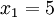
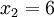
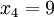
用 4 取代 N
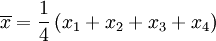
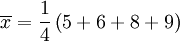
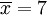此为平均值。
第二步，计算标准差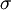
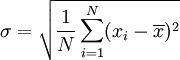
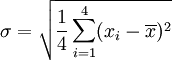用 4 取代 N
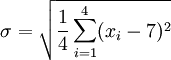用 7 取代
![\sigma = \sqrt{\frac{1}{4} \left [ (x_1 - 7)^2 + (x_2 - 7)^2 + (x_3 - 7)^2 + (x_4 - 7)^2 \right ] }](/picture/bkimg/ch_90/90_6_85_20.jpg)
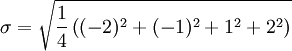
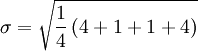
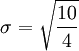
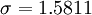
标准差与平均值之间的关系
一组数据的平均值及标准差常常同时做为参考的依据。在直觉上，如果数值的中心以平均值来考虑，则标准差为统计分布之一"自然"的测量。较确切的叙述为：假设 x1, ..., xn 为实数，定义其公式
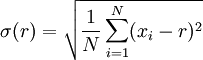
使用微积分，不难算出 σ(r) 在下面情况下具有唯一最小值：
