1) sine basic function


正弦基函数
1.
The relations between the amplitude-frequency response of Type-three FIR filter with linear phase and the algorithm of neural network based on sine basic functions are studied.
详细研究了3型FIR线性相位滤波器的幅频响应与正弦基函数神经网络算法之间的关系,提出并证明了该模型算法的收敛性定理,给出了3型FIR带通滤波器、海尔伯特变换器和微分器的优化设计实例。
2) sinusoidal interpolate basis


正弦插值基函数
1.
By using the sinusoidal interpolate basis and Daubechies discrete wavelet transform,the computing time is considerably reduced.
文中采用一种新的粗圆柱线天线快速精确计算模型 ,提出了所谓的“等长分段”方法 ,并使用了一种固定间隔电压源模型 ,大大提高了分析计算的精度 ;通过使用正弦插值基函数、引入Daubechies小波变换等 ,提高了分析计算的速度 。
3) sine function


正弦函数
1.
The Development of the Courseware of Applying Visual Basic Language to Simulating "Drawing Image of Sine Function with Sine Line";
利用Visual Basic语言模拟“用正弦线作正弦函数图象”的课件开发
2.
Draw Sine Function Image with Computer;


计算机绘制正弦函数图象
3.
On some identities of sine and cosine functions;


关于正弦函数和余弦函数的一些恒等式
4) sinusoidal function


正弦函数
1.
The numerical expression of trigonometric function and its approximate expression are discussed in detail,a kind of analog electric circuit for sinusoidal function is designed using analog multiplier/divider,and the direct analog circuits for the computation of the attitude parameters with negative feedback are also presented.
根据旋转导向钻井工具姿态参数的求解需要,结合Taylor中值定理,提出一种模拟解算方法,分析了三角函数的展开式及其逼近表达式,并应用模拟乘法/除法器和负反馈电路设计了正弦函数拟合求解和姿态参数角直接解算电路。
2.
This paper presents a new model of chaotic neural network whose activation func- tion is composite of Sinusoidal function and Sigmoid function by analyzing the bifurcation process and Lyapunov exponent spectrum.
通过复合正弦函数和Sigmoid函数构成激励函数,构造了一种新的暂态混沌神经网络。
5) sine basis functions neural networks


正弦基函数神经网络
1.
This paper presents the model of sine basis functions neural networks based on BP learning algorithm,gives the convergence condition of the neural networks algorithm and studies optimal design example of the type three FIR band-pass filters with a linear phase.
提出了一种基于BP学习算法的正弦基函数神经网络模型,给出了该网络系统的收敛性条件,研究了3型线性相位FIR带通滤波器优化设计实例。
6) sine radial basis function (SRBF)


正弦型径向基函数(SRBF)
补充资料:反正弦函数
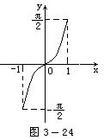
函数y=sinx的反函数叫做反正弦函数,记作x=arcsiny.
习惯上用x表示自变量,用y表示函数,所以反正弦函数写成y=arcsinx.
定义域是[-1,1],值域是y∈[-∏/2,∏/2];
arcsinx的含义:
(1) 这里的x满足 ;
(2) arcsinx是 (主值区)上的一个角(弧度数);分得再细一点,即当 时, ;当 时, 。
(3) 这个角(弧度数)的正弦值等于x,即sin(arcsinx)=x.
函数图象:我们知道这个结论“函数y=f(x)的图象和它的反函数y=f-1(x)的图象关于直线y=x对称”,先画出函数y=sinx在 上的图象,用平板玻璃或透明纸画好图象,翻转过来,从图象上我们可以得到以下两个结论:
(1) 反正弦函数y=arcsinx在区间[-1,1]上是增函数;
(2) 反正弦函数y=arcsinx的图象关于原点对称,这说明它是奇函数,也就是arcsin(-x)=-arcsinx,x∈[-1,1].
说明:补充资料仅用于学习参考,请勿用于其它任何用途。