1) Bernstein power series operator


Bernstein幂级数算子
1.
On the limiting properties of Bernstein power series operator;


Bernstein幂级数算子的极限性质
2) powers of Bernstein operators


Bernstein 算子幂
3) Bernstein-Sikkema Operators


Bernstein-Sikkema算子
1.
Lipschitz Property of Bivariate Bernstein-Sikkema Operators;


定义了正方形和单纯形上的二元Bernstein-Sikkema算子,研究了其一个重要的性质:函数与算子属于同一个Lipschitz类,其结果包含了文献《正方形上的Lipschitz连续函数的Bernstein多项式的常数Lipschitz》中的结果。
4) Durrmeyer-Bernstein operators


Durrmeyer-Bernstein算子
5) Bernstein-Durrmeyer operators


Bernstein-Durrmeyer算子
1.
Equivalence characterization for derivatives of Bernstein-Durrmeyer operators;


Bernstein-Durrmeyer算子导数的等价刻划
2.
As an application, the relationship between the multivariate Bernstein-Durrmeyer operators defined on the simplex and the modulus is discussed as well.
作为应用,讨论定义在单纯形上多元Bernstein-Durrmeyer算子与多元加权光滑模之间的关系。
3.
Secondly, a modification of Bernstein-Durrmeyer operators are introduced and the related approximation properties are also studied.
本文首先研究了一类修正的Bernstein算子的点态逼近性质,其次对Bernstein-Durrmeyer算子进行了修正,并研究了它的逼近性质。
6) Bernstein operators


Bernstein算子
1.
On approximation by Meyer-Konig and Zeller operators and Bernstein operators in interpolation spaces;
Meyer-Konig and Zeller算子及Bernstein算子在内插空间中的逼近
2.
The best polynomial approximation and degree of weighted approximation of multivariate Bernstein operators;
最佳多项式逼近与多元Bernstein算子的加权逼近阶
3.
Simultaneous approximation by Bernstein operators;


Bernstein算子的同时逼近
补充资料:幂级数
| 幂级数 power series 一个无穷阶的多项式。又称为泰勒级数。它的一般形式是a0+a1(z-z0)+…+an(z-z0)n+…=  ak(z-z0)k ,其中系数ak ,z0及变量z均可取复数值 ,幂级数的收敛域是一个圆盘 ,它可能收缩退化为一个点z=z0 ,也可能扩张为整个复平面,当圆盘有界时,则幂级数在此圆盘的闭面之外一定发散,而在圆盘的边界上,幂级数的和函数至少有一个奇点,即这一点任意一个领域都不能成原来的收敛圆盘的解析开拓圆盘(见解析函数)。将收敛圆盘的半径称为幂级数的收敛半径。 ak(z-z0)k ,其中系数ak ,z0及变量z均可取复数值 ,幂级数的收敛域是一个圆盘 ,它可能收缩退化为一个点z=z0 ,也可能扩张为整个复平面,当圆盘有界时,则幂级数在此圆盘的闭面之外一定发散,而在圆盘的边界上,幂级数的和函数至少有一个奇点,即这一点任意一个领域都不能成原来的收敛圆盘的解析开拓圆盘(见解析函数)。将收敛圆盘的半径称为幂级数的收敛半径。有一种幂级数 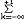 ak(z-z0)k 可能在一个圆的外部 :|z-z0|>r收敛,若同时还有 ak(z-z0)k 可能在一个圆的外部 :|z-z0|>r收敛,若同时还有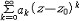 在圆|z-z0|<R上收敛,且 r<R,则级数 在圆|z-z0|<R上收敛,且 r<R,则级数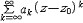 就在圆环 r<|z-z0|<R上收敛,这样的幂级数称为罗朗级数,其中的负幂部分称为它的主要部分,而余下的部分称为解析部分,当一个收敛的罗朗级数的收敛圆环的内圆收缩退化为一个点时,这个点称为罗朗级数和函数(这是一个解析函数)的孤立奇点,若罗朗级数的主要部分为零,则称这一奇点为可去奇点,若主要部分有有限多项,则称该点为和函数的本性奇点,若主要部分因有无限多项 ,则称其为本性奇点 。 一种特殊情形 就在圆环 r<|z-z0|<R上收敛,这样的幂级数称为罗朗级数,其中的负幂部分称为它的主要部分,而余下的部分称为解析部分,当一个收敛的罗朗级数的收敛圆环的内圆收缩退化为一个点时,这个点称为罗朗级数和函数(这是一个解析函数)的孤立奇点,若罗朗级数的主要部分为零,则称这一奇点为可去奇点,若主要部分有有限多项,则称该点为和函数的本性奇点,若主要部分因有无限多项 ,则称其为本性奇点 。 一种特殊情形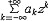 在|z|>R收敛于 f(z),则称它为 f(z) 在∞点的罗朗级数,这时称它的正幂部分为主要部分,而其余的部分为解析部分。同样,当主要部分仅有有限多项时,称∞为该级数和函数的极点,当主要部分有无限多项时,称∞为本性奇点。 在|z|>R收敛于 f(z),则称它为 f(z) 在∞点的罗朗级数,这时称它的正幂部分为主要部分,而其余的部分为解析部分。同样,当主要部分仅有有限多项时,称∞为该级数和函数的极点,当主要部分有无限多项时,称∞为本性奇点。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条