1) harmonic progression and p-progressive


调和级数与p-级数
2) harmonic series


调和级数
1.
Divergence and Application of Harmonic Series;


调和级数的发散及其应用
2.
This paper put forward a recurrence formula through calculation and synthesis,based an harmonic series theory.
通过计算、综合、证明等步骤,得出飞机空中加油问题的递推公式,并以调和级数等相应的数学理论为基础来解决。
3.
A proof of existence of primitive functions of a continuous function with area principle is introduced,and the divergence of the harmonic series in area method is also proved.
用面积原理证明了原函数存在定理;给出了调和级数发散性的面积方法证明。
3) harmonic progression


调和级数
1.
Research into Convergency in the Subset of Harmonic Progression;


对调和级数子集收敛性的研究
2.
Harmonic Progression and Various Prove Method


调和级数及其发散性的多种证法
3.
The harmonic progression is more important divergent series in the theory of series.


调和级数是级数理论中一种比较重要的发散级数,现行《数学分析》教材中,有关它的发散性证明学生在学习中不易掌握。
4) P-series


P-级数
1.
An Estimation on Partial Sum of a Divergent P-series;


发散的P-级数部分和的一个估计
2.
A Further Estimation on Remaider of a Converge P-series;


收敛的P-级数余项的进一步估计
3.
There are many ways to prove that P-series converges when p>1 and diverges when 0<p≤1.
P-级数(广义调和级数)+∞n=1移n1p当p>1时收敛,当0
5) p progression


p级数
1.
A Brief Proof for Convergence and Divergence of Harmonic progression and P progression


调和级数与P级数敛散性的简单证法
6) p-series field


p级数域
补充资料:级数
| 级数 series 将数列un的项 u1,u2,…,un,…依次用加号连接起来的函数。数项级数的简称。如:u1+u2+…+un+…,简写为 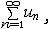 un称为级数的通项,记 un称为级数的通项,记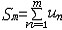 称之为级数的部分和。如果当m→∞时 ,数列Sm有极限S,则说级数收敛,并以S为其和,记为 称之为级数的部分和。如果当m→∞时 ,数列Sm有极限S,则说级数收敛,并以S为其和,记为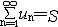 否则就说级数发散。级数是研究函数的一个重要工具,在理论上和实际应用中都处于重要地位,这是因为:一方面能借助级数表示许多常用的非初等函数, 微分方程的解就常用级数表示;另一方面又可将函数表为级数,从而借助级数去研究函数,例如用幂级数研究非初等函数,以及进行近似计算等。级数的收敛问题是级数理论的基本问题。从级数的收敛概念可知,级数的敛散性是借助于其部分和数列Sm的敛散性来定义的。因此可从数列收敛的柯西准则得出级数收敛的柯西准则 : 否则就说级数发散。级数是研究函数的一个重要工具,在理论上和实际应用中都处于重要地位,这是因为:一方面能借助级数表示许多常用的非初等函数, 微分方程的解就常用级数表示;另一方面又可将函数表为级数,从而借助级数去研究函数,例如用幂级数研究非初等函数,以及进行近似计算等。级数的收敛问题是级数理论的基本问题。从级数的收敛概念可知,级数的敛散性是借助于其部分和数列Sm的敛散性来定义的。因此可从数列收敛的柯西准则得出级数收敛的柯西准则 :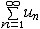 收敛 收敛 任意给定正数ε,必有自然数N,当n>N时 ,对一切自然数 p,有|un+1+un+2+…+un+p|<ε,即充分靠后的任意一段和的绝对值可任意小。 任意给定正数ε,必有自然数N,当n>N时 ,对一切自然数 p,有|un+1+un+2+…+un+p|<ε,即充分靠后的任意一段和的绝对值可任意小。如果每一un≥0(或un≤0),则称 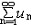 为正(或负)项级数,正项级数与负项级数统称为同号级数。正项级数收敛的充要条件是其部分和序列Sm 有上界,例如 为正(或负)项级数,正项级数与负项级数统称为同号级数。正项级数收敛的充要条件是其部分和序列Sm 有上界,例如 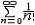 收敛,因 为 收敛,因 为 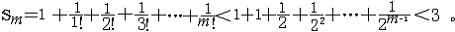 有无穷多项为正,无穷多项为负的级数称为变号级数,其中最简单的是形如 有无穷多项为正,无穷多项为负的级数称为变号级数,其中最简单的是形如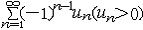 的级数,称之为交错级数。判别这类级数收敛的基本方法是莱布尼兹判别法 :若un ≥un+1 ,对每一n∈N成立,并且 的级数,称之为交错级数。判别这类级数收敛的基本方法是莱布尼兹判别法 :若un ≥un+1 ,对每一n∈N成立,并且 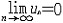 ,则交错级数收敛。例如 ,则交错级数收敛。例如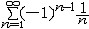 收敛。对于一般的变号级数如果有 收敛。对于一般的变号级数如果有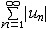 收敛,则称变号级数绝对收敛。如果只有 收敛,则称变号级数绝对收敛。如果只有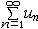 收敛,但是 收敛,但是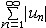 发散,则称变号级数条件收敛。例如 发散,则称变号级数条件收敛。例如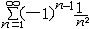 绝对收敛,而 绝对收敛,而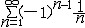 只是条件收敛。 只是条件收敛。 如果级数的每一项依赖于变量 x,x 在某区间I内变化,即un=un(x),x∈I,则称 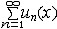 为函数项级数,简称函数级数。若x=x0使数项级数 为函数项级数,简称函数级数。若x=x0使数项级数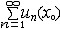 收敛,就称x0为收敛点,由收敛点组成的集合称为收敛域,若对每一x∈I,级数 收敛,就称x0为收敛点,由收敛点组成的集合称为收敛域,若对每一x∈I,级数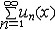 都收敛,就称I为收敛区间。显然,函数级数在其收敛域内定义了一个函数,称之为和函数S(x),即 都收敛,就称I为收敛区间。显然,函数级数在其收敛域内定义了一个函数,称之为和函数S(x),即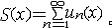 如果满足更强的条件, 如果满足更强的条件,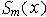 在收敛域内一致收敛于S(x)。 在收敛域内一致收敛于S(x)。一类重要的函数级数是形如 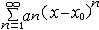 的级数,称之为幂级数 。它的结构简单 ,收敛域是一个以 的级数,称之为幂级数 。它的结构简单 ,收敛域是一个以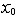 为中心的区间(不一定包括端点),并且在一定范围内具有类似多项式的性质,在收敛区间内能进行逐项微分和逐项积分等运算。例如幂级数 为中心的区间(不一定包括端点),并且在一定范围内具有类似多项式的性质,在收敛区间内能进行逐项微分和逐项积分等运算。例如幂级数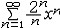 的收敛区间是 的收敛区间是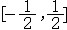 ,幂级数 ,幂级数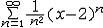 的收敛区间是[1,3],而幂级数 的收敛区间是[1,3],而幂级数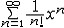 在实数轴上收敛。 在实数轴上收敛。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条